
Author: William Li
Mentor: Dr. Osman Yağan
Stuyvesant High School
Abstract
The robustness of networks has become an essential field of study as our modern society creates increasingly complex systems. Failure in these networks can have disastrous consequences, making it critical to understand and improve different systems. Over the past two decades, research on the robustness of different systems has progressed extensively, ranging from single-network models to cyber-physical interdependent systems. Albert, Jeong, & Barabási (2000) showed that scale-free networks are robust against random failures but vulnerable to targeted attacks in purely structural models. Motter & Lai (2002) expanded this by modeling physical systems with load redistribution and cascading failures. Buldyrev et al. (2010) extended robustness research to interdependent networks, finding that coupled systems are more vulnerable to failures than isolated systems. Finally, Zhang & Yağan (2016) addressed more realistic cyber-physical systems, finding equal redundant space in nodes to be beneficial. This literature review pieces the papers together to highlight the growing complexity of models in robustness research.
Introduction
With the technological advancements of the modern world, we have become increasingly reliant on complex networks such as the Internet, power grids, transportation systems, communication networks, and numerous others that support our way of life. In these networks, the failure of even a small fraction of nodes can result in disastrous collapses. Generally, robustness in a network is defined as its ability to maintain functionality when nodes or links are removed either by random failures or targeted attacks. Thus, network robustness has become a critical topic of study in order to understand and prevent failures. Over the course of the past two decades, research on network robustness has progressed from simple models of single cyber networks to sophisticated interdependent cyber-physical systems. This paper reviews four fundamental papers that display such progression and highlights the findings of each study and how they have advanced our understanding of robustness in realistic settings.
Attack and Error Tolerance of Complex Networks – Albert, Jeong & Barabási (2000)
Albert, Jeong, and Barabási analyzed the robustness of single networks with a particular emphasis on scale-free networks. In scale-free networks, the degree distribution P(k) follows a power-law. Simplified, this means that in such networks the majority of nodes have a small number of edges to other nodes (low degree), and a few nodes known as hubs have extremely high degrees, i.e., have a large number of connections. Some examples of scale-free networks include the Internet, airline networks, social networks, and even biological systems such as metabolic networks. In contrast to scale-free networks, Erdős–Rényi networks follow an exponential degree distribution, resulting in the lack of the hubs that exist in scale-free networks. While scale-free networks are common in real life, Erdős–Rényi networks rarely occur naturally. Instead, they are used as a baseline model to be used in research and sometimes in controlled scientific experiments. See Figure 1 for an illustration of both networks.

The paper defines the interconnectedness of a network by a diameter d, defined as the average length of the shortest paths between any two nodes in the network. A smaller diameter means a more connected network. In this paper, robustness is defined as a network’s ability to preserve its giant component (a connected subgraph containing a significant fraction of the nodes) and low diameter as a function of the fraction f of nodes removed. They quantify this in their models using the size of the giant component, and the network diameter. The simulations in this paper showed that scale-free networks are extremely robust to random failures. This is because in a scale-free network, there is a low probability of selecting a hub, which is vital to maintaining a low diameter within the network. Since the randomly selected node is often a low degree node, removing such a node with few connections would have little impact on the network. However, the existence of hubs in scale-free networks is the reason why the paper finds that targeted attacks on the network are devastating. Since hubs are vital to the diameter of the network, specifically removing these hubs would rapidly reduce the connectivity in the network. Scale-free networks show no failure threshold against random failures, but display a sharp critical threshold (abrupt collapse) under targeted attacks. The paper also finds that in Erdős–Rényi networks, random failures and targeted attacks essentially have the same effect. Most of the nodes in an Erdős–Rényi network have a degree close to the average, so when any one of these nodes are removed, there is no dramatic impact on the connectivity of the network. Both random failures and targeted attacks gradually fragment the network. The nature and findings of this study are particularly interesting because it established a foundation that the hubs in a scale-free network make it extremely robust to random failures but also vulnerable to targeted attacks. However, the networks examined in this paper are purely structural, disregarding systems that may be subject to overload-based failures. This classic paper by Albert, Jeong, and Barabási introduces a limitation to later be addressed by studies using load-based models for scale-free networks.
Cascade-based Attacks on Complex Networks – Motter & Lai (2002)
Similar to the work of Albert, Jeong, and Barabási, this study by Motter & Lai studies the robustness of single networks but introduces the concept of load-based cascading failures. This approach is more realistic, as many real-world systems operate under distribution of load or flow. Examples include power grids, transportation systems, and communication networks. Motter & Lai use a physical network to evaluate the robustness of scale-free networks against failures that cause flow redistribution to other nodes. They define the capacity of a node as the maximum load that a node can handle, with the initial load being the total number of shortest paths passing through the node. The capacity C_j of node j is proportional to its initial load L_j, giving us the equation C_j = (1 + α) L_j, where the tolerance parameter α adds extra capacity to a node (α >= 0). In this paper, robustness is defined as the network’s ability to survive load-based cascades triggered by removals, and is quantified by the relative size of the largest connected component after the cascade. When a node fails, the shortest paths in the new structure of the network are recalculated. The node’s load is then redistributed along those paths. If this additional load causes some node’s total load to exceed its capacity, that node will also fail. Such subsequent failures can lead to more failures, which is called a cascade that can propagate through a network. Motter and Lai find that scale-free networks are especially vulnerable to cascading failures when hubs in the network are removed. The nature of scale-free networks results in a heterogeneous distribution of loads, resulting in hubs carrying a disproportionately large share of load. Therefore, removing a hub and redistributing its large load is likely to cause many nodes to exceed their capacity, leading to a cascade of failures. However, Motter and Lai also find from their models that increasing the average degree in a network increases its robustness, which makes sense as the redistribution of a removed node’s load would be spread across more nodes. This would reduce the impact of a cascade since the remaining nodes would be taking on less load and thus be less likely to exceed its capacity. This study expands the concept of robustness in single networks to include physical systems with load-redistribution. By accounting for this, Motter and Lai’s paper addresses a limitation of Albert, Jeong, and Barabási’s work and provides a deeper understanding of real-world systems that transport physical flows.
Catastrophic cascade of failures in interdependent networks – Buldyrev et al. (2010)
While the previous papers are both foundational to the study of network robustness, they focus on single complex networks. However, modern systems are often not standalone, but rather coupled. Buldyrev et al. expands the study of robustness into interdependent systems, in which two networks are dependent on one another through dependency links. In Buldyrev et al.’s paper, two networks A and B are modeled. Each node in A depends on one node in B, and each node in B depends on one node in A; see Figure 2 for an illustration of their interdependent system model.
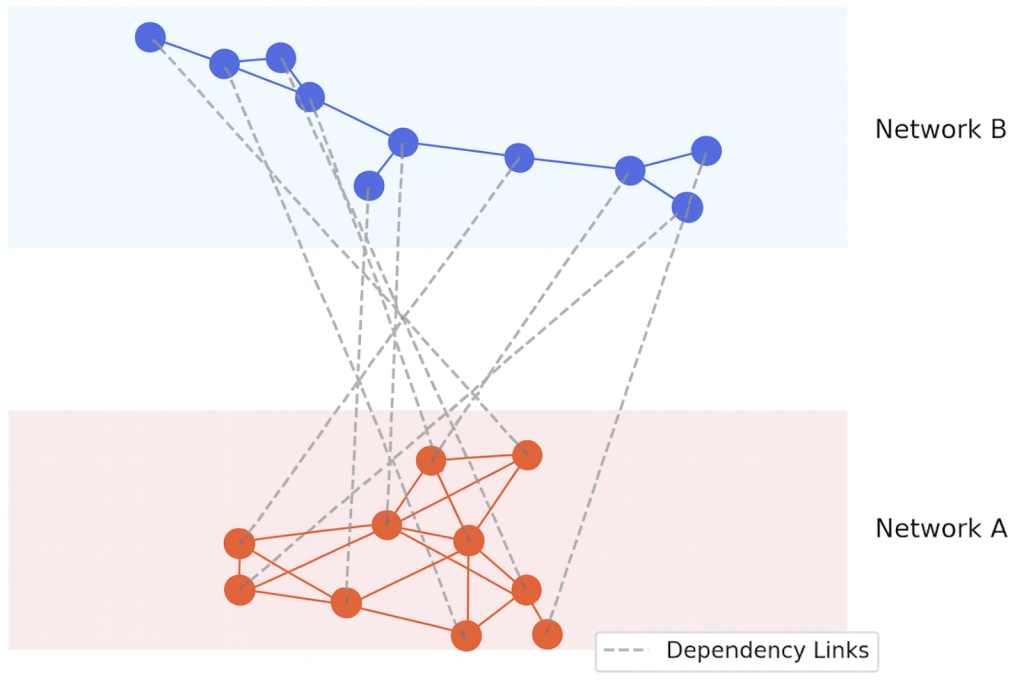
If a node in A were to fail, its dependent node in B would also fail, and vice versa. It is important to note that both of these systems are cyber systems, meaning their connectivity is purely structural and does not consider load or flow. The robustness is simulated by a cascade process which begins by removing a fraction of nodes from network A. After this initial attack, nodes in A that are no longer part of the giant component are removed. Next, nodes in network B are removed based on the dependency links between the nodes of A and B. Any nodes in B that are not part of the giant component are also removed, which in turn removes the dependent nodes in A. This process continues until a giant mutually connected component (GMCC) appears or the network collapses. A GMCC is defined as the largest set of nodes that are connected within their own networks A and B and also have their interdependent nodes in the other network still functioning. Buldyrev et al. find that interdependent networks are far more fragile than single networks. In their model, it is found that removing even a small fraction of nodes can cause a complete collapse of both systems. Interestingly, interdependent scale-free networks are also vulnerable to random failures (recall that single scale-free networks are robust to these failures) because of the possibility that a node connected to a hub is removed, causing the hub to be removed through its dependency link. This study marks a shift in the understanding of robustness by showing the impact of interdependency on networks. Previous work on single networks emphasized either structural or load-based vulnerabilities, but Buldyrev et al. demonstrated that networks that are resilient when examined alone can be extremely fragile when coupled with another.
Robustness of Interdependent Cyber-Physical Systems against Cascading Failures – Zhang & Yağan (2016)
Similar to Buldyrev et al.’s study of interdependent networks, Zhang & Yağan examine the robustness of two coupled systems. However, instead of modeling both as purely structural networks, they introduce a cyber-physical interdependent system: a cyber network which operates based off structural connectivity, where functionality depends on connection to giant component, and a physical network that follows load-based principles, similar to the system examined by Motter & Lai. The two networks are connected through random one to one dependency links. The cascade process begins with a random attack on the physical network A, which removes a fraction of its nodes. Network A then undergoes a load-based update in which failed nodes redistribute their loads among all remaining nodes (which has a similar effect to redistributing among neighboring nodes only) and subsequent failures can follow. Failures in A then spread to B through dependency links, removing the corresponding nodes. Since B is a cyber system, any nodes that are not part of the giant component are removed. The failures in B are simulated by using one random attack on the network. Once failures in B are done, they spread back to A through dependency links and this process is repeated until the interdependent system is either collapsed or in a steady state where no new failures are occurring. Zhang & Yağan find that the robustness of the interdependent system increases when each of the nodes in the physical network has the same redundant space (capacity minus initial load). Redundant space is the extra capacity a node has in addition to its initial load. This work extends robustness research from interdependent networks in which both networks follow the same failure principles to more realistic cyber-physical systems with fundamentally different networks.
Discussion
Throughout these four papers, the study of network robustness progresses from single networks to interdependent systems. Cyber networks based on structural connectivity are examined alongside physical networks with load-based principles, and eventually evolve into interdependent cyber-physical systems. Albert, Jeong & Barabási find that scale-free networks are robust against random failures but vulnerable against targeted attacks. However, unlike the purely structural model used by Albert et al., Motter & Lai model physical systems with load redistribution to examine cascades in the real world more realistically. Similarly to the preceding paper, they find that scale-free networks are extremely vulnerable against targeted attacks. While these papers address both physical and cyber systems, they are limited because they focus on single networks rather than interdependent systems. As interdependency has become increasingly prevalent in modern systems, Buldyrev et al. extended robustness research by modeling coupled networks using interdependency links between two networks, finding that interdependent systems are far more vulnerable than single networks due to propagation of failures between two networks. While this paper was fundamental in understanding the robustness of interdependent systems, it used two identical networks. Because most interdependent systems are now cyber-physical, Zhang & Yağan address this gap by modeling a cyber-physical system in which the two networks have different failure principles. They find that robustness can be increased when nodes are given equal redundant space. These four papers depict the progression in our understanding of network robustness, from single structural networks to load-based networks and expanding into interdependent systems.
Conclusion
The study of network robustness has advanced significantly over the past two decades, reflecting the growth of modern systems and their needs. From structural models of single networks to complex cyber-physical interdependent systems, each stage of robustness research has revealed new vulnerabilities and suggested new mitigation strategies. Albert, Jeong & Barabási set the basis for the robustness and fragility of scale-free networks under different attacks, while Motter & Lai used physical systems to model networks in a more realistic setting. Buldyrev et al. showed the weakness of interdependent networks, and Zhang & Yağan extended this line of work to interdependent cyber-physical systems. These works highlight the growing understanding of robustness and also the limitations that are addressed over time. With continued advancement of technologies ranging from smart power grids, Internet of Things, global communication infrastructures, and electrified transportation systems, robustness research will remain an essential field of study to address their potential vulnerabilities and prevent exploitation.
References
Réka Albert, Hawoong Jeong, and Albert-László Barabási. “Error and Attack Tolerance of Complex Networks.” Nature, vol. 406, no. 6794, July 2000, pp. 378–382, https://doi.org/10.1038/35019019.
Sergey V. Buldyrev, Roni Parshani, Gerald Paul, H. Eugene Stanley, and Shlomo Havlin. “Catastrophic Cascade of Failures in Interdependent Networks.” Nature, vol. 464, no. 7291, Apr. 2010, pp. 1025–1028, https://doi.org/10.1038/nature08932.
Adilson E. Motter and Ying-Cheng Lai. “Cascade-Based Attacks on Complex Networks.” Physical Review E, vol. 66, no. 6, 20 Dec. 2002, https://doi.org/10.1103/physreve.66.065102.
Yingrui Zhang and Osman Yağan. “Robustness of Interdependent Cyber-Physical Systems against Cascading Failures.” IEEE Transactions on Automatic Control, vol. 65, no. 2, Feb. 2020, pp. 711–726, https://doi.org/10.1109/tac.2019.2918120.
About the author

William Li
