Electricity and Electric Phenomena

By Nathaniel ThornellPhysics

Author: Nathaniel Thornell
Mentor: Dr. Gino Del Ferraro
Cheyenne Central High School

Intro

Starting with the foundations of electricity, we briefly overview the foundation of a particle’s ability to have a charge and phenomena that come with different charges interacting. We qualitatively and quantitatively examine their interaction through forces, fields, flux, electric potential, and capacitance. Most sections are broken into subcategories to explain nuances and provide examples. Multiple figures are used as visual assistance to a descriptive section. Throughout the paper gravity was used as a reference subject because I have previous knowledge pertaining to Newtonian physics and because equations about gravity are symmetrical with equations about charges.

Forces and Fields are both defined as vectors in Physics, so vectors are important to understand electricity. Vectors are also beneficial because they have easy ways to add, subtract, multiply, and divide. Several other calculations like scalar and vector multiplication can also be used with vectors to find important quantities.

Introduction to Vectors

Vectors contain magnitude and direction. For forces and fields this means that they have a relative position and value in space. The properties of vectors are similar to the properties of an arrow drawn on a coordinate plane. A vector needs a point of reference or an origin just like an origin on a cartesian plane. With a point on a 2-D plane having two coordinates (x,y) and three coordinates on a 3-D plane (x,y,z), vectors can be represented as an arrow drawn from the origin to a point.

Adding and Subtracting

When two vectors are drawn on a plane, addition or subtraction of the two vectors can be shown graphically. When adding, a line that is parallel to vector A is drawn from the end point of vector B. After the same is done to vector A, then the intersection of both constructed segments represents the quantities of the summed vectors. The summed vector can then be drawn from the origin to the point of intersection. The complete structure forms a parallelogram structure; hence, the name of the method is parallelogram law of addition of vectors.

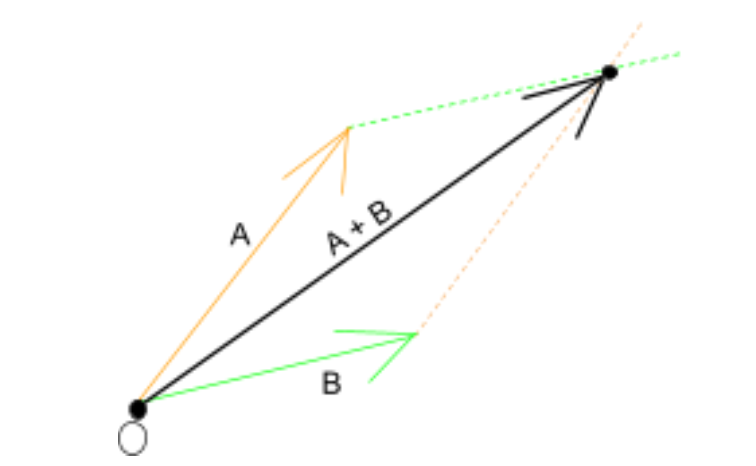
Figure 1. Vector A is in orange and vector B is in green. The origin is represented as a black dot and by the symbol O. The parallel lines drawn are dotted with their intersection being signified by another black dot. The summed vector is the vector represented by the black arrow.

For subtraction, the coordinate plane parallelogram structure can also be made to create a visual representation. The difference is seen in the subtlety that A-B = A + (-B). The opposite of a vector is the same as rotating it 180º about the origin or finding the opposites of the x and y coordinates.

Representations of Matrices in 2-D and 3-D

If exact coordinates are known, then the addition and subtraction can also be represented by matrix addition and subtraction. If vector A has coordinates of (3,4) and vector B has coordinates of (2,1), then A + B =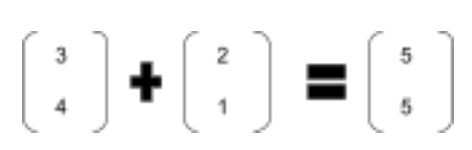

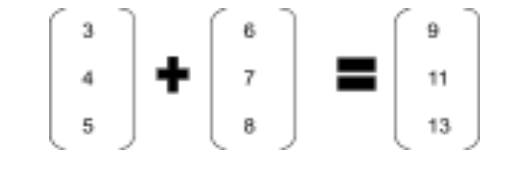
Vectors with three values can be represented by 3-D space. A value for x, y, and z. While a parallelogram figure cannot be constructed, 3 × 1 matrices can be used. A vector with coordinates of (3,4,5) and another of (6,7,8) can be added as shown below.

Coulomb’s Law

Ever since some materials were discovered to have qualities that attract and repel other objects, there has been a need to quantize the phenomena. Through experiments, Coulomb found that relationships between two particles with this weird property depended on a constant, the charges of the particles, and the distance between them. Coulomb’s equation to model the force that two charges can have on each other is F = k · \qaqb\ / r2 . This equation has the same properties as Newton’s law of gravitation where F = G · m1m2 / r2. The derivation of the equation to account for the force on one particle to another and the direction of that force is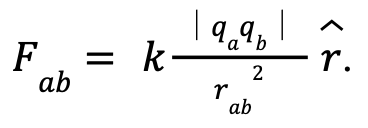

Meaning of k

Meaning of F

F is the force in newtons of the charges from particle a on particle b or vice versa. Since the force that particle a does on particle b is equal and magnitude and opposite in direction according to Newton’s third law, the forces must be distinguished. Fab represents the force that particle a experiences by particle b.

Meaning of r

Multiple Forces

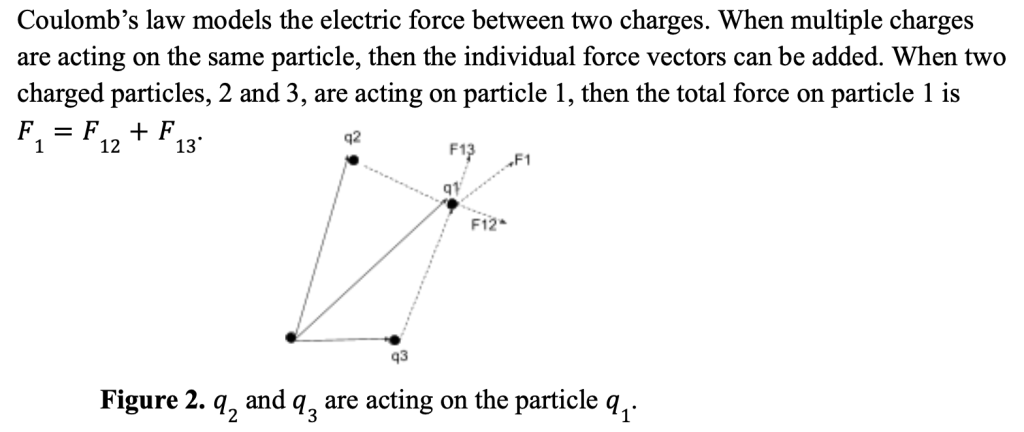
Electric Field

Coulomb’s law requires two particles to create a force, but can there be a force with only one particle? When one of the two particles travels farther and farther away, the electric coulomb force between them becomes weaker until almost nonexistent. Now, if we progressively bring this particle closer and closer to the other particle, a Force will come into existence and automatically enact. Therefore, this force exists when there is only one particle carrying charge.

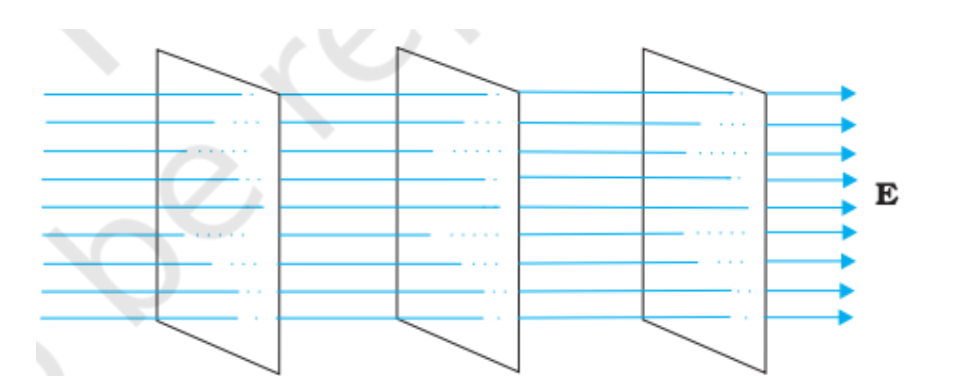
Since the electric field’s existence was proved in the previous section, we now need a way to visually represent it. Electric and gravitational fields can be represented by lines and arrows. Each arrow represents the direction of the field at that point in space.

Electric Field Lines

Single Particles

When one particle is considered in the representation of an electric field, the direction of the arrows depends on whether the charge is negative or positive. If the charge is positive, then the arrows will be facing away from the particle. If the charge is negative, then the arrows will be facing towards the particle.

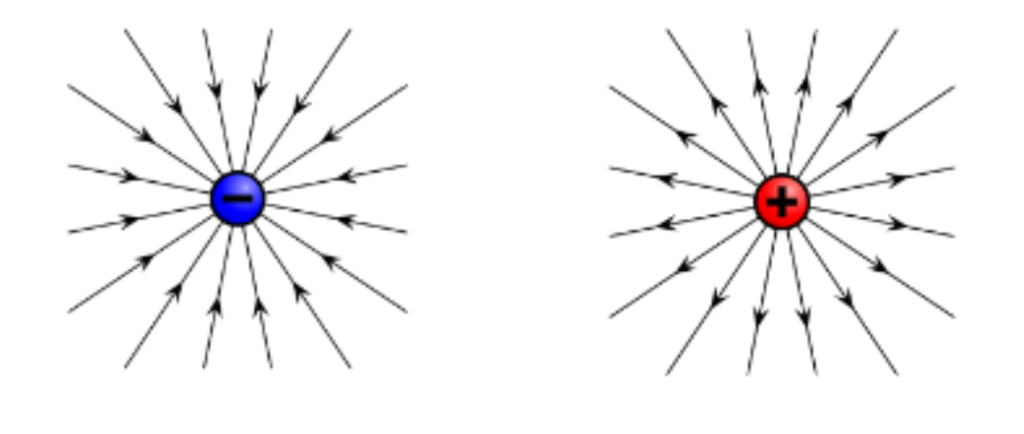
Figure 3. The negatively charged particle on the left has field lines going in but outward lines for the positive charge. Taken from [2].

In Fig 3, the distance of each of the arrows is the same distance away from the center of the particle, so the force of the electric field is equal in magnitude at each arrow. In 3-D space, a hypothetical sphere surrounds a particle and equidistance faces contain forces of equal magnitudes.

Two Particles

When two particles are at play, they create different models of electric field lines. When field lines are closer together, it symbolizes a stronger field. When they are further apart, the field is weaker.

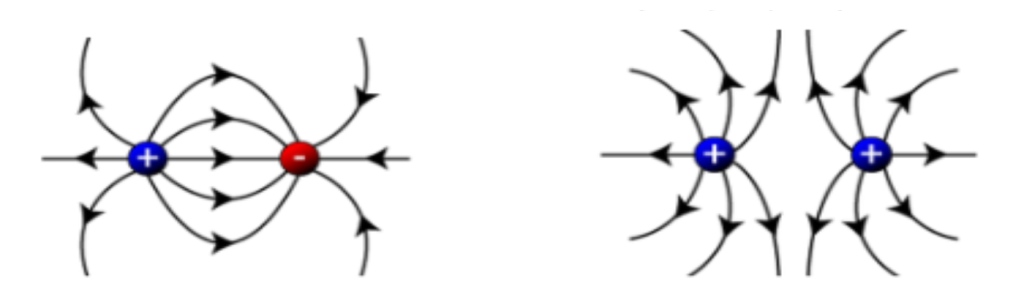
Figure 4. (Left) With oppositely charged particles, the force flows from the positive particle to the negative particle because electric field lines go out of positively charged particles and into negatively charged particles. The outsides of the image represent the same phenomenon when there would be only one particle. (Right) With similarly charged particles, field lines shoot up and away from the particles like asymptotes. The outsides of the image still represent the field lines when only one particle is present. With two negatively charged particles, the depiction is the same, but reversed arrow direction. Taken from [3].

Electric Flux

We know how to calculate the forces and electric fields exerted by one or multiple particles, but fields cannot exist in a surface. Therefore, to quantify the electric field in a surface, electric flux is found.

Understanding Flux

Flux can be better understood when thought of like water. If there is a stream with water flowing to the right and a surface/plane that is in the middle, then flux is the force that the surface feels or the amount of water that is passing through it. When the surface is perpendicular to the stream, then the flux is at a maximum. When the surface is parallel with the stream, then flux is at a minimum. The important quantities when determining flux are the normal (the line perpendicular to the plane) of the surface and the angle between the normal and the direction of the electric field.

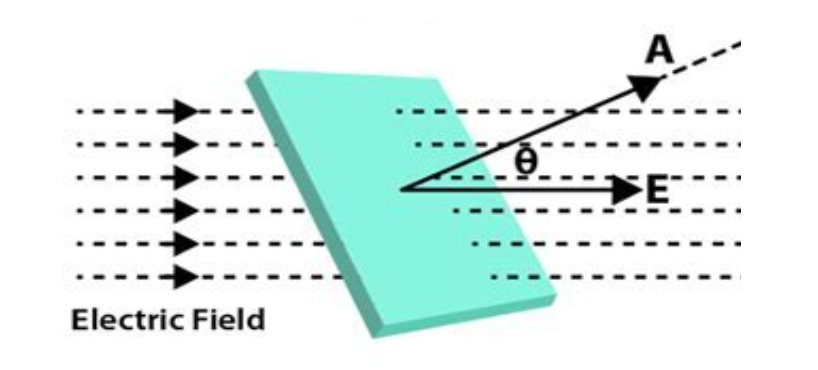
Figure 5. The electric field is going right towards the plane. The normal of the plane, A, is at an angle, θ, from the direction of the electric field. Taken from [4].

Quantifying Flux

Electric Dipoles

The reason dipoles are important to scientists is because they are found in molecules like H2O. Water has a hydrogen bond with its two hydrogen atoms which creates a dipole. Calculating the force of the charges between dipoles is needed for the study of atoms.

Calculating a Positive and Negative Dipole

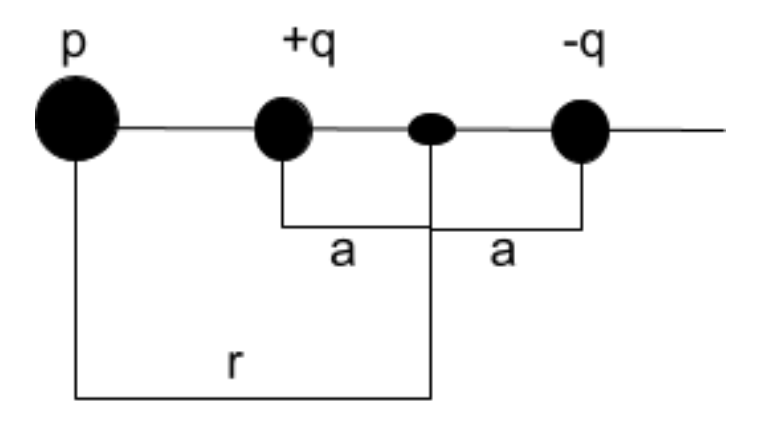
The simplistic form of a dipole is with one negative charge and one positive charge on the same plane with a point p. The charges are a distance, a, from the origin. The point, p, is a distance r from the origin so that p is r-a from the positive charge and r+a from the negative charge.

Figure 6. The point of concern is point p which is being acted on by the dipole.

Dipoles in an Electric Field

Combining the electric field and dipoles helps represent how the electric field acts in useful instances. When a dipole with a positively and a negatively charged particle has the charges acting on each other, the force can be represented as a vector line traveling from the negative charge to the positive charge. When this is put into an electric field, each charge also reacts to the field. Since the positive and negative charges react oppositely to the field, they go in different directions. This makes the dipole system spin counterclockwise or clockwise which creates torque on the system.

Figure 7. The positive electric field is pointing to the right and towards the dipole. The r represents the position vector between the two particles in the dipole. With the top particle being positively charged and the bottom particle being negatively charged, the top particle is repelled by the electric field and the bottom particle is attracted. This creates a clockwise rotating effect on the dipole.

Torque of a Dipole in a Field

Figure 8. With p representing a and E representing b, the right hand rule shows the direction of the torque or resultant a x b. Taken from [5].

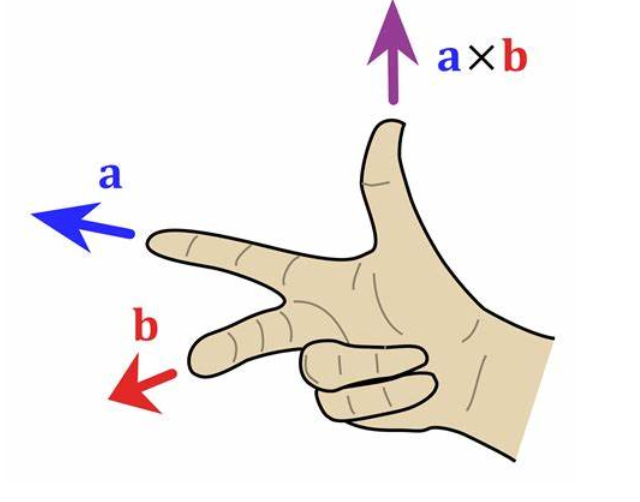
Vector Product

Continuous Charge Distribution

One Dimensional

Two Dimensional

Three Dimensional

Gauss’ Law

The purpose of Gauss’ Law is to try and quantify the amount of flux that any body/surface experiences with an electric field traveling through it.

Proof of Gauss’ Law

Examples

With a charged particle inside of a sphere, the particle creates an electric field. This field passes through the surface of the sphere creating a flux. To measure the flux, the sphere is broken up into several surfaces labeled Δs. The flux at each Δs is calculated, and then added to find the total flux in the sphere.

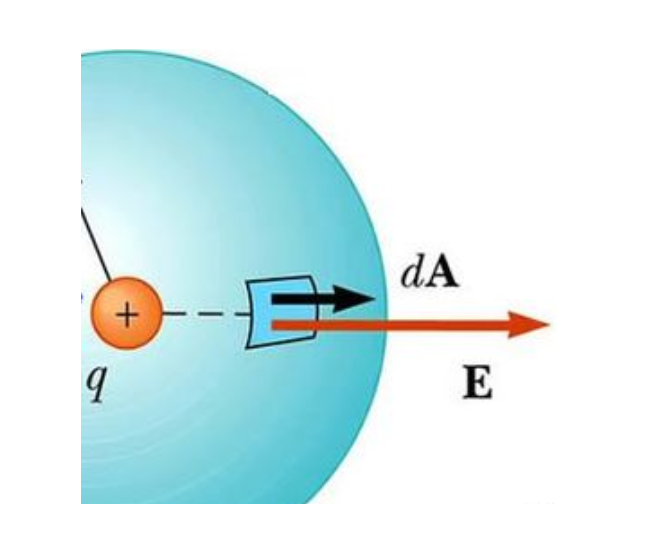
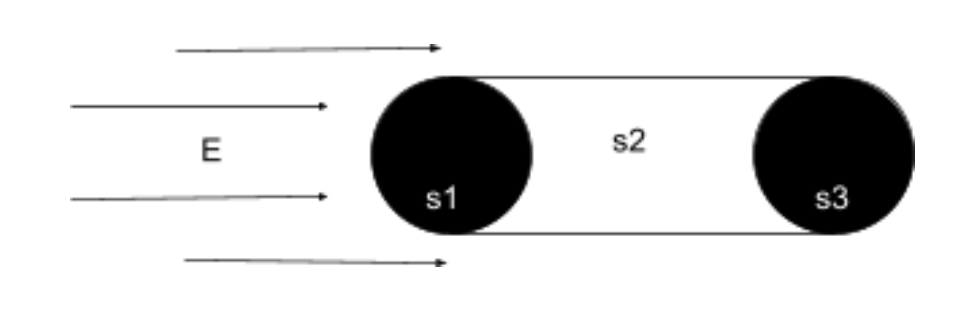
Figure 9. With the positively charged particle in the center of the sphere, it creates an electric field, E, that goes through the surface. The sphere is broken up into parts dA, which is equivalent to Δs, to make it possible to find the total flux of the sphere. Taken from [6].
Figure 10. The electric field, E, is acting upon the cylinder from the outside heading towards the area of s1. The outsides, s1 and s3, are identical while the main body is contained in the volume s2

Gauss’ Law is very important. Its importance can be seen in these applications of manipulating his formula to find resulting formulas for the electric field.

Solving for the Electric Field

One Dimensional Application

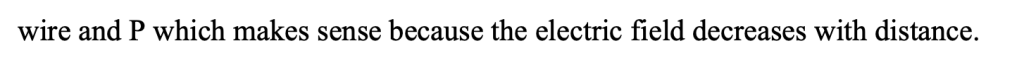
Two Dimensional Application

Work

Proving Electric Energy

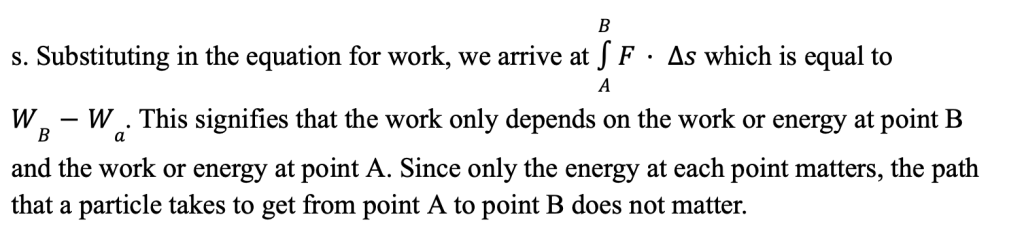
Proving Electric Energy

Figure 11. If the hiker takes route 1, 2, or 3, then the backpack dropped at the top will have the same amount of energy in all situations. Taken from [7].

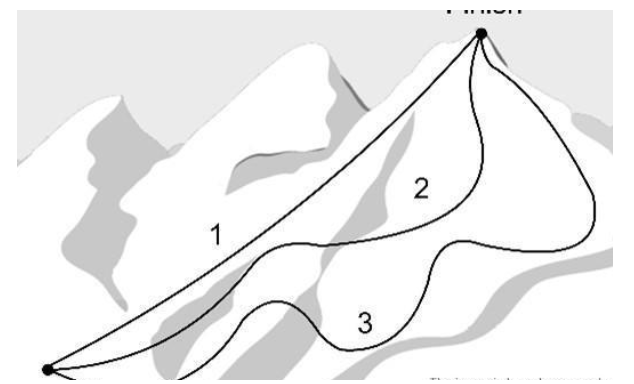
Since the route does not matter, it means that electrical and gravitational forces are conservative forces. The work only depends on the starting and ending positions because it is conserved regardless of the path.

Solving for Work

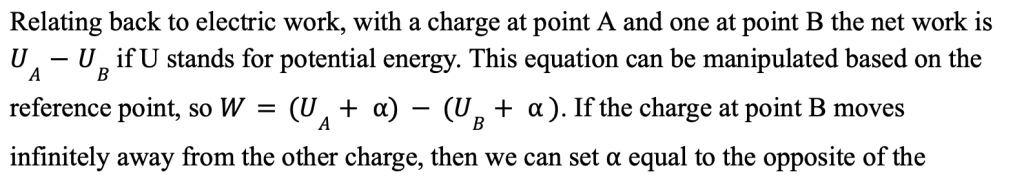
Finding Electric Potential

Point Charge

Figure 12. The graph displays two functions: 1/r which is blue and 1/r2 which is gray. The blue function represents the relationship between the electric potential, V, and the distance to the point P, r. The gray function represents the relationship between the electric field, E, and r. Taken from [1].

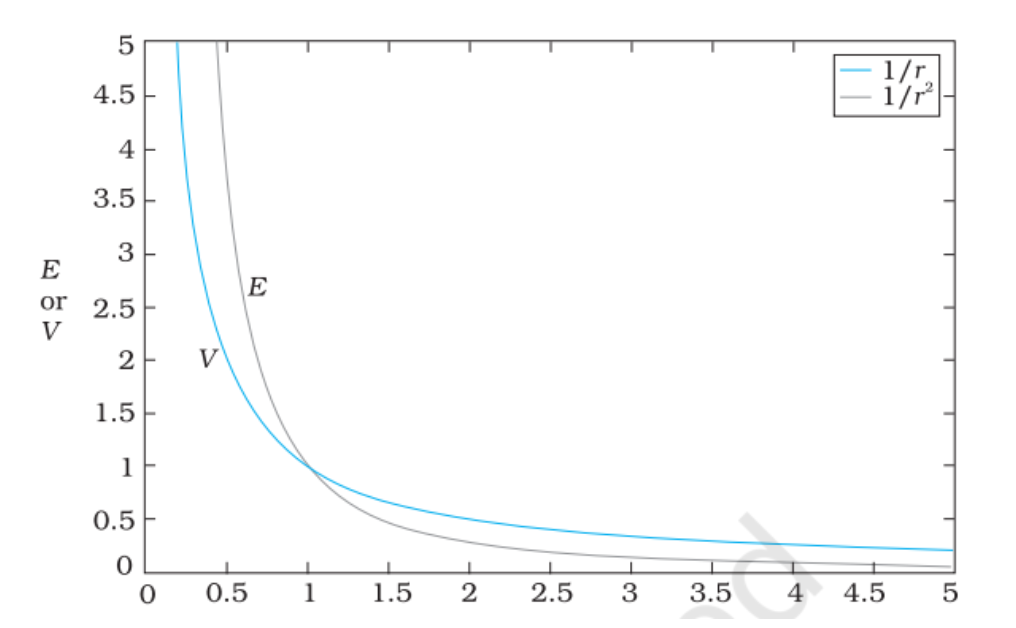
Electric potential and the electric field have a similar, but different relationship with r. They both decrease when r increases, but electric potential decreases slower as the r gets larger.

Dipole

Figure 13. p is the point dipole, O is the origin, P is the point, a is the distance between each charge and the origin, r is the distance between the origin and the point, and θ is the angle between the origin and the point. Taken from [1].

System of Charges

When multiple charges are acting on the same point, the net force that the point experiences can be calculated by summing the force exerted by each individual charge. This is also the same for an electric field: E = E1 + E2 + E3… Even though electric potential is a scalar quantity, it holds the same principles V = V1 + V2 + V3… This is important because generalizations can be made about the electric potential of systems of charges.

Equipotential Surfaces

One of the generalizations is equipotential surfaces. With a single charge, the equipotential surfaces are the same as circles surrounding the charge. Similarly, a 2-D plane containing a uniform charge will have equipotential surfaces that are square or rectangular and parallel to the charged plane.

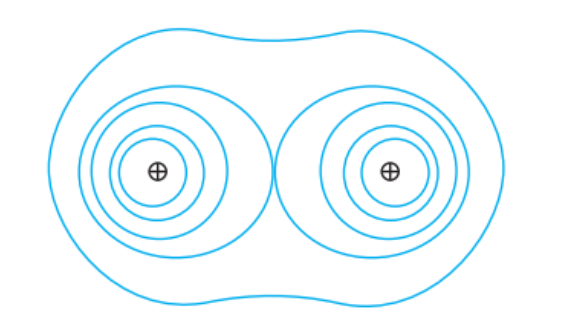
Figure 14. Each plane consists of infinitely many points that are an equal distance away from the charged 2-D plane. Each point on the same plane experiences the same electric field, so it creates an equipotential surface in the shape of a square or rectangle. Taken from [1].

Isoipse Lines

Equipotential surfaces can also be described as isoipse lines from a topographical map. The closer the lines, the steeper the change in elevation. In a similar manner, closer lines around a charge signify a greater force. Each line around a dipole or charge represents all the points that feel the same amount of charge.

Figure 15. The dipole system shown has two identical charges. In the middle of the diagram, the lines are not as close as the left edge and right edge, so the charge is weaker in the middle. Taken from [1].

Conductors

Conductors, usually metal, have a quality that allows electrons to pass through them easily. This lets electrons flow and a current to form. Conductors still follow Gauss’ law, so they cannot have an electrostatic field within. The electrostatic field is always zero because the same amount of field that enters will exit. Because they can have no internal electrostatic field, the surface has to always be normal to the electric field. The electrons on the surface or outside of it can experience a force and field.

Electrostatic Shielding

Since an electric field can exist on the surface of a conductor but not the outside, the field on the outside builds a shield like property. If there is a cavity inside the conductor, the electric field can still not exist inside when there is no internal charge. With the electrostatic shield protecting cavities inside, an external charge will not affect the conductor or the cavity. This is taken advantage of in daily life by Tracuit mountain huts and Faraday cages.

Figure 16. (Left) Tracuit mountain huts are made of metal conductors, so they create electrostatic shielding when lightning strikes. It dissipates the electric force on the surface, so that the interior cavity of rooms is not affected. Taken from [8].
(Right) A faraday cage is a cage made out of a conductor. The large object in the left of the picture creates high voltage that triggers small lightning hitting the Faraday cage. The cage uses electrostatic shielding to protect the people inside. Taken from [9].

Capacitance and Capacitors

Definition of Capacitance

Capacitors are made of two conductors separated by an insulator like air. The conductors contain opposite charges and an electric potential. The electric potential is proportional to the charge of the two conductors, so capacitance can be defined as C = Q/V. Since the charge and electric potential depend on each other, the only factor that changes the capacitance is the shape and configuration of the two conductors.

Parallel Plate Capacitors

Parallel plate capacitors is a capacitor that contains two parallel plate conductors of opposite charges separated by a small distance. Since the plates are of opposite charge, electrons flow from the positive conductor to the negative conductor. To calculate the electric field we can use the continuous charge distribution formula for a 2-D surface because the plates act as 2-D objects.

Figure 17. The top plate conductor contains a positive charge, and the bottom plate conductor contains a negative charge. The electric field is flowing from positive to negative. Taken from [1].

Series and Parallel

References

[1] NCERT. (2006). Physics: Textbook for class XII 2 parts. National Council Of Education Research and Training.

[2] Course hero. Boundless Physics | | Course Hero. (n.d.). https://www.coursehero.com/study-guides/boundless-physics/the-electric-field-revisited/

[3]https://physics.stackexchange.com/questions/288172/why-is-electric-field-lines-away-from-an d-toward

[4] Physics Wallah. (2023, July 26). What is electric flux – definition, formula, unit, symbol: PW. Physics Wallah. https://www.pw.live/physics-articles/what-is-electric-flux

[5] Take online courses. earn college credit. Research Schools, Degrees & Careers. Study.com | Take Online Courses. Earn College Credit. Research Schools, Degrees & Careers. (n.d.). https://study.com/academy/lesson/cross-product-right-hand-rule-definition-formula-examples.ht ml

[6] Gauss’s law to Coulomb’s law: Physics and Mathematics, Gauss’s law, learn physics. Pinterest. (2020, June 13). https://www.pinterest.com/pin/591730838531027476/

[7] Three hikers take three different paths to the top of a … – brainly.com. (n.d.). https://brainly.com/question/19277682

[8] Cabane Tracuit: Wallis. AlpineWelten. (n.d.). https://www.alpinewelten.com/cabane-tracuit

[9] Staff. (2023, February 2). Faraday cage. Science Facts. https://www.sciencefacts.net/faraday-cage.html

About the author

Nathaniel Thornell

Nathaniel is currently a senior at Cheyenne Central High School. He enjoys physics and mathematics, as well as finding unique solutions to math problems, jigsaw puzzles, and Rubik’s cubes.