
Author: Alexander Yang
Mentor: Dr. Gino Del Ferraro
Livingston High School
Introduction
Objects and planets in space are much bigger than daily objects we encounter on Earth and, therefore, they experience much larger gravitational forces that cause them to orbit around, collapse on, or escape from another object. The motion of extraterrestrial objects has always intrigued me, especially the NASA DART project, which is a mission to protect the Earth from potential asteroids impacting its surface. I find the collision of objects in space very interesting because the trajectory of the objects after colliding has to take in so many factors like the mass of the objects, their velocities, and any surrounding objects.
Before I can explain more about the NASA DART project, however, I need to introduce the basics of gravitation and space physics. I will explain the different parts of space physics, like Newton’s universal law of gravitation, the acceleration of objects due to gravitational forces of the Earth and other objects, and escape speed, the speed it takes for an object to escape an object’s orbit. I will also go into the concept of gravitational potential energy, the energy an object has while in orbit, the energy required to place an object in orbit, and the nature of objects orbiting Earth, also known as Earth satellites. Additionally, I will explain Johannes Kepler’s famous 3 laws of planetary motion for a better understanding of how planets move in space.
Finally, I will introduce the NASA DART (Double Asteroid Redirection Test), a mission where NASA tries to develop technology to protect the Earth in the unlikely event that an asteroid is headed for Earth. Their goal is to make an object, like a satellite, hit the asteroid, thus changing the trajectory of the asteroid and making it miss the Earth.
This report is also complemented by Python code that simulates planetary motion. It is available for download on my GitHub here: https://github.com/alyang21/solarsystem
2. Gravitation
2.1 Universal Law of Gravitation
On Earth, the acceleration at which an object falls toward the Earth is a constant 9.8 m/s2. However, this rate is different on other extraterrestrial objects. This is because the force of gravity exerted on an object depends on its mass as well as the mass of the objects around it. Knowing this, famed physicist Sir Issac Newton derived the Universal Law of Gravitation in 1687 [8]. His equation is

where G is the universal gravitational constant, at 6.67 x 10-11. Furthermore, this equation suggests that the force depends on both objects’ masses and how far apart they are separated. In vector form, the equation can be written as

Furthermore, the sum of the forces on an object by the surrounding objects is just the vector sum of all the forces.
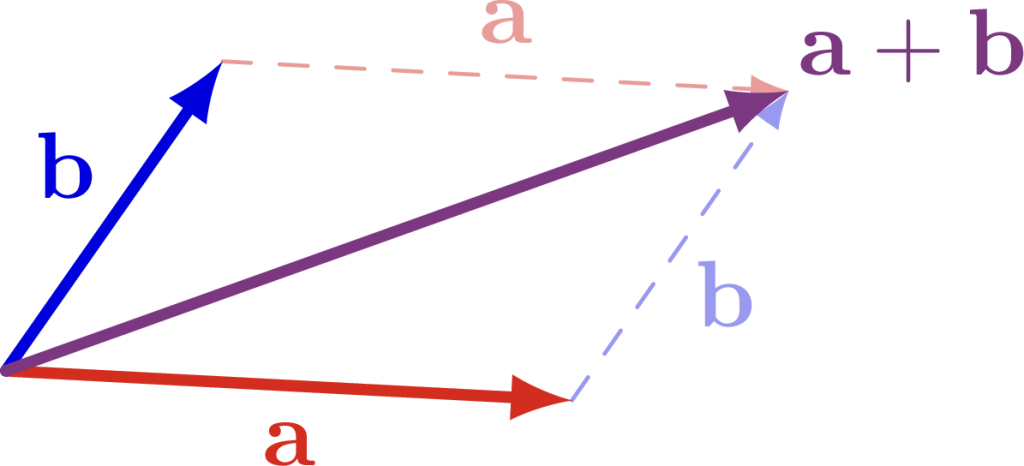
Figure 1.1 The sum of two vectors is found by placing the two vectors tail to tip, and the resulting vector is from the tail of the first vector to the tip of the second. [1]
2.2 Acceleration Due to Gravity of the Earth
The Earth can be visualized as a number of spherical shells centered at the same point. Since the mass of all the shells combined is the mass of the Earth, and the force of gravity by the Earth comes from the center of the Earth. By taking into account the Earth’s density using its volume and mass, we can derive that the force of gravity by the Earth on an object is Fg = (GMEm)/RE2 [8]. Since Fg = mg where g is the acceleration by the Earth according to Newton’s second Law,

2.3 Gravitational Potential Energy
The gravitational potential energy of an object on Earth depends on its distance from the center of the Earth. We also know that work equals force multiplied by displacement, so the work done by the Earth to bring a body of mass m from the height h2 to the height h1 is given by:

In other words, the work done on an object is the difference of potential energy from the initial to final positions of the object. If we say that the potential energy W(h) at a height h above the surface of the Earth so that W(h) = mgh + W0 where W0 is a constant, then W12 = W(h2) – W(h1) [8]. It is also important to note that h = 0 means points on the surface of the Earth.
If we lift the particle along a vertical path where r1 is the distance from the center of the Earth at its first point and r2 is the distance from the center at its second point, then we get

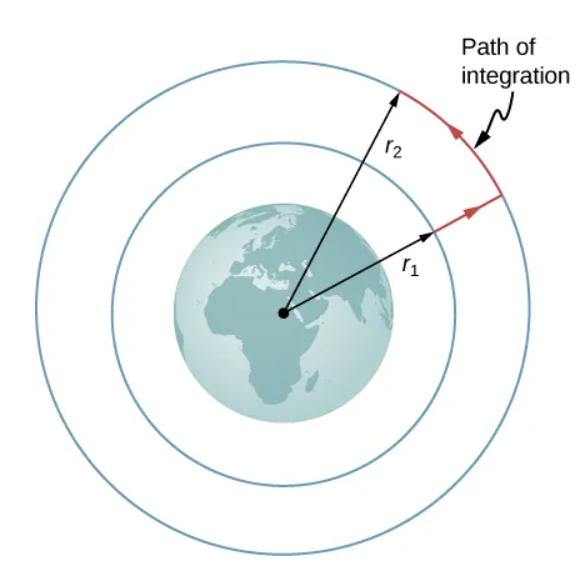
And as a result,

2.4 Escape Speed
Using the law of conservation of energy, we can find the escape speed for an object out of a planet, or the speed it needs to break through the pull of the planet [8]. If we can find the distance where the object has no more potential energy and only kinetic energy, we can set the energies of the object at those two points equal to each other, thus allowing us to find the initial velocity that the object has to leave the planet with.

As long as the final velocity is greater than or equal to 0, the object can reach infinity. So,

The initial velocity is the minimum velocity for the object to escape the atmosphere, so

If the object is thrown from the surface of the Earth, h = 0, and

Thus, we come to the equation

where RE is the radius of the Earth. This means that the escape speed is independent of the object’s own mass. Additionally, with the knowledge of the Earth’s radius, we can find that the escape speed is 11.2 km/s.
2.5 Earth Satellites
Earth satellites are objects which revolve around the Earth, usually in the shape of an ellipse. The Moon is the only natural satellite of the Earth, and it has a near-circular orbit. Other satellites have been sent up by humans for telecommunication, geophysics, and meteorology. To find the period that these satellites orbit around the Earth once, we can use the equation for centripetal force, where m is the mass of the satellite and V is its speed [8].

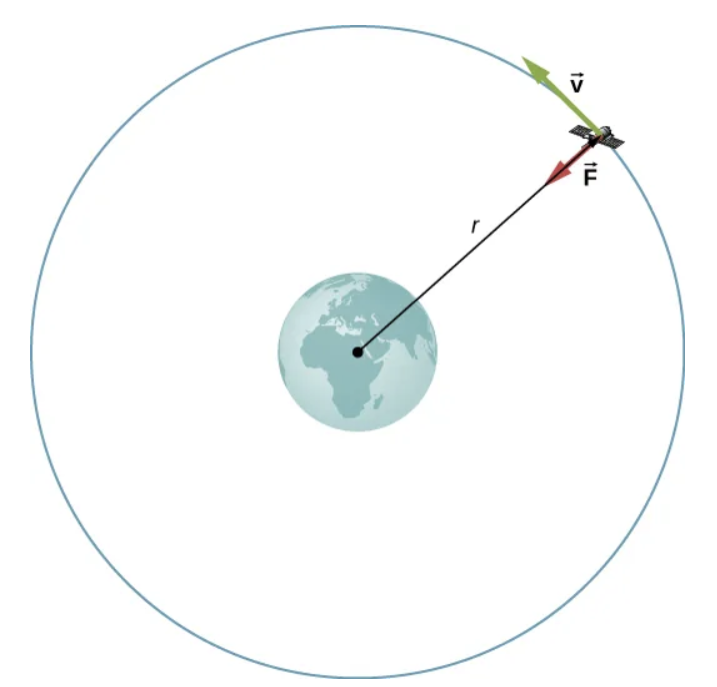
This centripetal force is provided by the gravitational force, similar to equation (1.1) but after substituting the variables for the mass and radius of the Earth, we get

Setting the two equations together, we find that

A satellite travels a distance 2πRE with speed V if the satellite is so close to the Earth’s surface that h can be neglected. The time period the satellite takes to orbit the Earth therefore is

and using the relation g = GM/RE2, we arrive at the equation

Substituting the numerical values, we get

Which is about 85 minutes.
2.6 Energy of an Orbiting Satellite

Notice how K is positive and Ug is negative. When added up, the total energy of the satellite is

It makes sense that the satellite’s total energy is negative because if the total energy is positive, it would leave the orbit and escape to infinity.
2.7 Energy Required to Orbit a Satellite

The energy required to put a satellite into Earth’s orbit is the difference between the satellite’s total energy in orbit and its energy at Earth’s surface. For example, if we want to lift the 9000-kg Soyuz vehicle from the Earth’s surface up to the ISS, which is 400 km above the Earth’s surface, we would have to find its energy at the Earth’s surface, as well as its total energy in orbit at the ISS. Using Eq 1.19, we get that the total energy of the Soyuz in the same orbit as the ISS is where m is 9000 kg and h is 0. Plugging the numbers in, we get that Eorbit is -2.65 x 1011 J. The total energy at the surface is just -GmMe/Re because Esurface = Ksurface + Usurface and Ksurface is 0. Plugging the numbers in, we get Esurface = -5.63 x 1011 J. As explained earlier, the energy required is the change in energy, so the energy required is = -2.65 x 1011 – (-5.63 x 1011) = 2.98 x 1011 J [8].
2.8 Kepler’s Laws of Planetary Motion
After German astronomer Johannes Kepler obtained the data collected by Tycho Brahe, he was able to analyze the positions of all the known planets and our moon. He realized that the orbits of the planets around the sun were elliptical, and was able to come up with three basic laws of planetary motion [8].
Kepler’s first law states that all planets orbit along an ellipse, where the Sun is one of the foci of the ellipse. An ellipse is the set of all points where the sum of the distance from each point to the two foci is a constant.
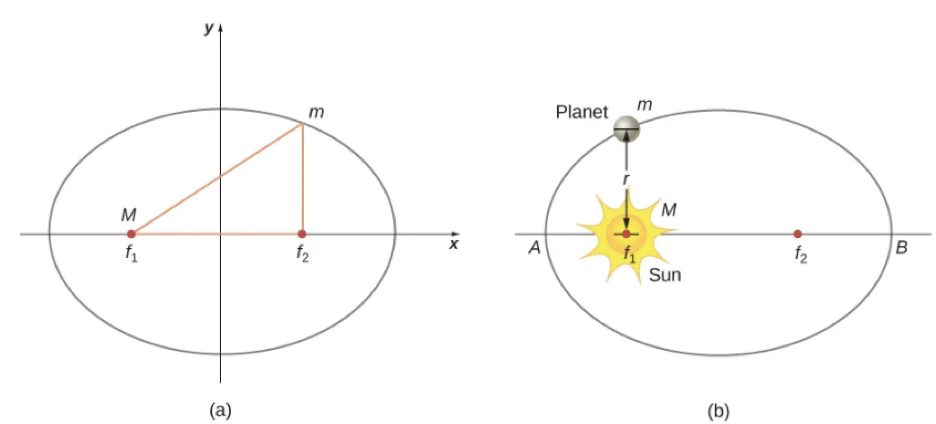
In an elliptical orbit, the point where the planet is the closest to the Sun is called the perihelion, which is represented by point A in Figure 1.4. The figure also shows point B, the farthest point from the Sun. This point is called the aphelion.
The ellipse is a specific example of a conic section, given by the equation

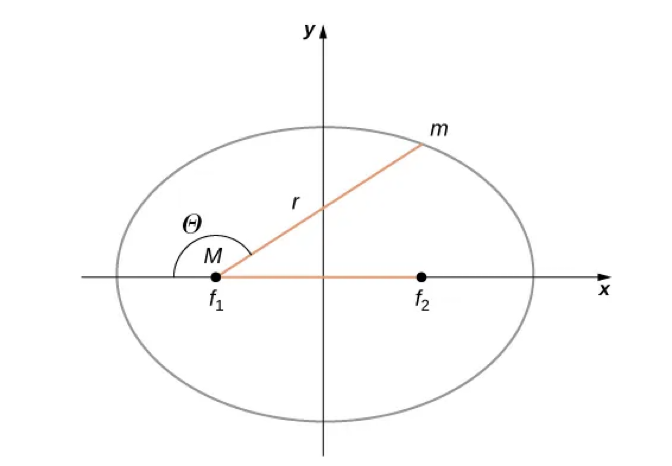
The variables r and θ from Eq. 1.20 are shown in Figure 1.5. The other two variables, and e, are constants determined by the total energy and angular momentum of the satellite at a point on the ellipse. The constant e is the eccentricity, which determines how close to being a circle the ellipse is. The closer to 0, the more circular the ellipse is, and the closer to 1, the flatter it is.
Kepler’s second law states that over equal periods of time, a planet will sweep out equal areas. In other words, the area it sweeps divided by the time, also known as the areal velocity, is a constant.
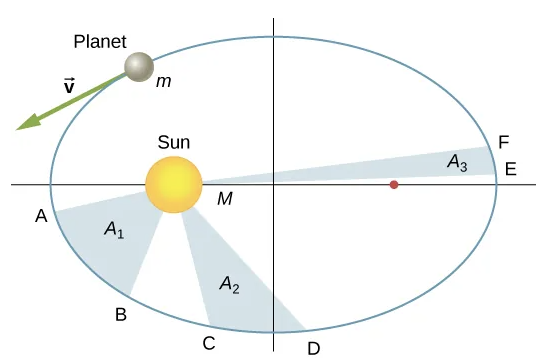
This makes sense when you consider that when the planet is closer to the Sun, it is moving faster. Since the energy of the planet-sun system is conserved, when the planet gets closer to the sun, its gravitational potential energy decreases, so its kinetic energy and velocity must increase.
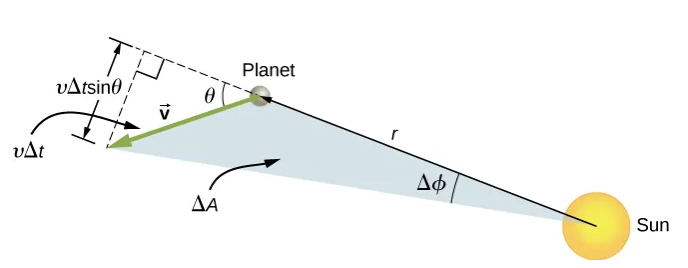
Figure 1.7 The area ∂ swept out during time as the planet moves through angle . The angle between the radial direction of r and is . [4]
Kepler’s third law states that the square of the period is proportional to the cube of the semi-major axis of the orbit. For this law, we have the equation

In this equation, a is the semi-major axis of the ellipse and T is the period. Interestingly, this law can also be derived from Newtonian principles and the principle of conservation of energy [8]. Additionally, his equation applies to any satellite orbiting any large mass, not just our Sun. If we use this equation for a circular orbit of r about the Earth, we get

3. DART Project NASA
It is widely believed that millions of years ago, the dinosaurs were put into extinction when a meteoroid hit the surface of the Earth. Although no meteor has gotten close enough to Earth since then to cause humans to panic, the scientific community agrees that another meteor will eventually cross paths with the Earth. To combat this, NASA started the Double Asteroid Redirection Test, or DART, to see if it is possible to alter the course of an asteroid by sending an object to impact it.
I first learned about DART when I visited the Kennedy Space Center in Florida and watched a video about its mission. I was immediately intrigued by DART because I had an interest in object collisions from playing pool and baseball. The DART mission added an interesting element that wasn’t involved when playing on a flat billiards table: the gravitational force of other extraterrestrial objects. This mission pushed me to learn about gravitation, planetary motion, and overall space physics in order to understand the DART mission from a scientific perspective.
DART’s target is the binary asteroid system Didymos. Since Didymos is not on a path that would impact the Earth, it is the ideal candidate for the first planetary defense experiment. The impact would be safe, even if something were to go wrong. The asteroid system consists of two asteroids: the larger asteroid named Didymos, and its moonlet, Dimorphos. DART’s plan was to collide with the moonlet Dimorphos, and then we would examine the changes in Dimorphos’ orbit as a result of the impact.
The journey to Dimorphos was complicated and required many different state-of-the-art technologies. One was the Small-body Maneuvering Autonomous Real Time Navigation (SMART Nav), developed for guidance, navigation, and control (GNC). The system had to be autonomous because NASA cannot control a satellite when it is 11 million kilometers away from Earth. The system was able to distinguish between Didymos and Dimorphos, and accurately navigate to the moonlet, eventually colliding with the smaller asteroid. DART was also equipped with an ion propulsion system that is solar-powered and incredibly fuel-efficient. Speaking of solar-powered, DART had a Roll-Out Solar Array (ROSA), extending 8.5 meters in length on each side. These solar arrays were used before on the ISS, but DART was the first to use them on a planetary spacecraft. Finally, the LICIACube allowed the DART team back on Earth to see images of the impact and the ejecta cloud, helping them assess the impact and its effects on Dimorphos. These technologies, paired with great antennas to send and receive data from the satellite allowed the DART mission to be incredibly successful.


Figure 1.8 The three images above show the various technologies the DART satellite used throughout its mission. SMART Nav (left) helped the satellite accurately impact Dimorphos. ROSA (center) gave the satellite its power for its ion propulsion system (right). [5]
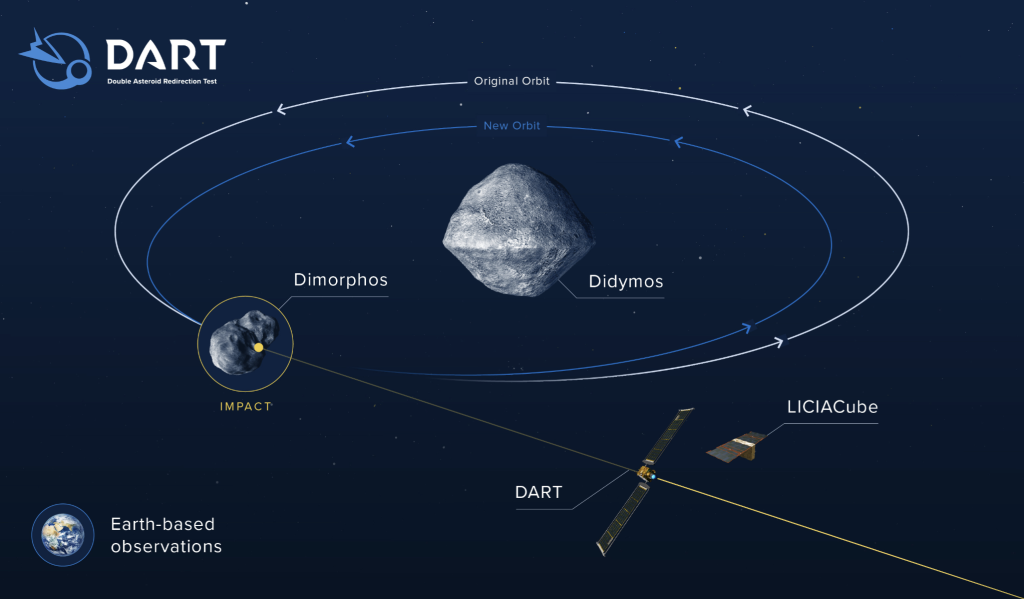
Figure 1.9 DART would impact Dimorphos from the direction Dimorphos is moving towards, slowing it down. This would cause Dimorphos’ new orbit to be closer to Didymos since its orbiting velocity decreased. At the same time, the LICIA Cube, which DART would eject 15 days before impact, would be able to capture images of the impact and send them back to Earth for NASA to examine. [6]
Overall, the DART project was a massive success, lifting off in November 2021 and colliding with Dimorphos in September 2022. However, the mission is not complete. The DART team is still examining the data from the impact in order to explore all the effects of the impact on Dimorphos. You can watch videos about the mission at this link: https://dart.jhuapl.edu/Gallery/ [7]
References
[1] https://tikz.net/vector_sum/
[2] https://openstax.org/books/university-physics-volume-1/pages/13-3-gravitational-potential-energy-and-total-energy
[3] https://openstax.org/books/university-physics-volume-1/pages/13-4-satellite-orbits-and-Energy
[4] https://openstax.org/books/university-physics-volume-1/pages/13-5-keplers-laws-of-Planetary-motion
[5] https://dart.jhuapl.edu/Mission/Impactor-Spacecraft.php
[6] https://dart.jhuapl.edu/Mission/index.php
[7] https://dart.jhuapl.edu/Gallery/
[8] This work is partially based on the content of this book: NCERT Books for Class 11 Physics, https://www.ncertbooks.guru/ncert-books-class-11-physics/amp/
Appendix
The following code computes the planetary motion of the Earth, Mars, and a fictional comet orbiting around the sun according to gravitational physics. The trajectories of these planets are calculated using Newton’s Universal Law of Gravitation, with given initial conditions for the position and velocities of each object. These trajectories are computed over a 5-year period and are visualized using an animation. The code is written in the Python language and is taken from this blog post: https://towardsdatascience.com/simulate-a-tiny-solar-system-with-python-fbbb68d8207b
Available on my Github page here: https://github.com/alyang21/solarsystem
# Ensure the right backend for Spyder
import matplotlib
matplotlib.use(“Qt5Agg”)
import matplotlib.pyplot as plt
from matplotlib import animation
# Constants and initial setup with constants and the objects’ masses, velocities, and gravitational constants.
G = 6.67e-11 # constant G
Ms = 2.0e30 # sun
Me = 5.972e24 # earth
Mm = 6.39e23 # mars
Mc = 6.39e20 # comet
AU = 1.5e11 # earth sun distance
daysec = 24.0*60*60 # seconds of a day
e_ap_v = 29290 # earth velocity at aphelion
m_ap_v = 21970 # mars velocity at aphelion
commet_v = 7000 # comet velocity
gravconst_e = G*Me*Ms
gravconst_m = G*Mm*Ms
gravconst_c = G*Mc*Ms
# Starting positions
# earth
xe, ye, ze = 1.0167*AU, 0, 0
xve, yve, zve = 0, e_ap_v, 0
# mars
xm, ym, zm = 1.666*AU, 0, 0
xvm, yvm, zvm = 0, m_ap_v, 0
#comet
xc, yc, zc = 2*AU, 0, 0
xvc, yvc, zvc = 0, commet_v, 0
# sun
xs, ys, zs = 0, 0, 0
xvs, yvs, zvs = 0, 0, 0
t = 0.0
dt = 1*daysec
# these lists store the points that the objects are at
xelist, yelist, zelist = [], [], []
xmlist, ymlist, zmlist = [], [], []
xclist, yclist, zclist = [], [], []
xslist, yslist, zslist = [], [], []
# save the initial position in their respective lists
#earth
xelist.append(xe)
yelist.append(ye)
zelist.append(ze)
#mars
xmlist.append(xm)
ymlist.append(ym)
zmlist.append(zm)
#comet
xclist.append(xc)
yclist.append(yc)
zclist.append(zc)
# Simulation
# The new radii, forces, velocities, and positions are calculated at each second for 5 years. The new position is then added to the object’s list.
while t < 5*365*daysec:
################ earth #############
# compute G force on earth
rx,ry,rz = xe – xs, ye – ys, ze – zs
modr3_e = (rx**2+ry**2+rz**2)**1.5
fx_e = -gravconst_e*rx/modr3_e
fy_e = -gravconst_e*ry/modr3_e
fz_e = -gravconst_e*rz/modr3_e
# update quantities how is this calculated? F = ma -> a = F/m
xve += fx_e*dt/Me
yve += fy_e*dt/Me
zve += fz_e*dt/Me
# update position
xe += xve*dt
ye += yve*dt
ze += zve*dt
# save the position in list
xelist.append(xe)
yelist.append(ye)
zelist.append(ze)
################ mars #############
# compute G force on mars
rx_m,ry_m,rz_m = xm – xs, ym – ys, zm – zs
modr3_m = (rx_m**2+ry_m**2+rz_m**2)**1.5
fx_m = -gravconst_m*rx_m/modr3_m
fy_m = -gravconst_m*ry_m/modr3_m
fz_m = -gravconst_m*rz_m/modr3_m
xvm += fx_m*dt/Mm
yvm += fy_m*dt/Mm
zvm += fz_m*dt/Mm
# update position
xm += xvm*dt
ym += yvm*dt
zm += zvm*dt
# save the position in list
xmlist.append(xm)
ymlist.append(ym)
zmlist.append(zm)
################ comet ##############
# compute G force on comet
rx_c,ry_c,rz_c = xc – xs, yc – ys, zc – zs
modr3_c = (rx_c**2+ry_c**2+rz_c**2)**1.5
fx_c = -gravconst_c*rx_c/modr3_c
fy_c = -gravconst_c*ry_c/modr3_c
fz_c = -gravconst_c*rz_c/modr3_c
xvc += fx_c*dt/Mc
yvc += fy_c*dt/Mc
zvc += fz_c*dt/Mc
# update position
xc += xvc*dt
yc += yvc*dt
zc += zvc*dt
# add to list
xclist.append(xc)
yclist.append(yc)
zclist.append(zc)
################ the sun ###########
# update quantities how is this calculated? F = ma -> a = F/m
xvs += -(fx_e+fx_m)*dt/Ms
yvs += -(fy_e+fy_m)*dt/Ms
zvs += -(fz_e+fz_m)*dt/Ms
# # update position
xs += xvs*dt
ys += yvs*dt
zs += zvs*dt
xslist.append(xs)
yslist.append(ys)
zslist.append(zs)
# update dt
t +=dt
print(‘data ready’)
# Animation setup
# grid size
fig, ax = plt.subplots(figsize=(6,6))
ax.set_aspect(‘equal’)
ax.grid()
# earth is blue. The text “Earth” follows point_e as it moves
line_e, = ax.plot([], [], lw=1, c=’blue’)
point_e, = ax.plot([AU], [0], marker=”o”, markersize=4, markeredgecolor=”blue”, markerfacecolor=”blue”)
text_e = ax.text(AU, 0, ‘Earth’)
# mars is red. The text “Mars” follows point_m as it moves
line_m, = ax.plot([], [], lw=1, c=’red’)
point_m, = ax.plot([1.666*AU], [0], marker=”o”, markersize=3, markeredgecolor=”red”, markerfacecolor=”red”)
text_m = ax.text(1.666*AU, 0, ‘Mars’)
# comet is black. The text “Comet” follows point_c as it moves
line_c, = ax.plot([],[], lw=1, c=’black’)
point_c, = ax.plot([2*AU], [0], marker=”o”, markersize=2, markeredgecolor=”black”, markerfacecolor=”black”)
text_c = ax.text(2*AU,0,’Comet’)
# the sun is yellow
point_s, = ax.plot([0], [0], marker=”o”, markersize=7, markeredgecolor=”yellow”, markerfacecolor=”yellow”)
text_s = ax.text(0, 0, ‘Sun’)
ax.axis(‘equal’)
ax.set_xlim(-3*AU, 3*AU)
ax.set_ylim(-3*AU, 3*AU)
exdata, eydata = [], []
mxdata, mydata = [], []
cxdata, cydata = [], []
# The points for each object are put into their respective data sets to be plotted on grid
def update(i):
exdata.append(xelist[i])
eydata.append(yelist[i])
mxdata.append(xmlist[i])
mydata.append(ymlist[i])
cxdata.append(xclist[i])
cydata.append(yclist[i])
line_e.set_data(exdata,eydata)
point_e.set_data(xelist[i],yelist[i])
text_e.set_position((xelist[i],yelist[i]))
line_m.set_data(mxdata,mydata)
point_m.set_data(xmlist[i],ymlist[i])
text_m.set_position((xmlist[i],ymlist[i]))
line_c.set_data(cxdata,cydata)
point_c.set_data(xclist[i],yclist[i])
text_c.set_position((xclist[i],yclist[i]))
point_s.set_data(xslist[i],yslist[i])
text_s.set_position((xslist[i],yslist[i]))
ax.axis(‘equal’)
ax.set_xlim(-3*AU,3*AU)
ax.set_ylim(-3*AU,3*AU)
#print(i)
return line_e,line_m,line_c,point_s,point_e,point_m,point_c,text_e,text_s,text_m,text_c
anim = animation.FuncAnimation(fig, func=update, frames=len(xelist), interval=1, blit=False)
plt.show(block=True)
About the author

Alexander Yang
Alex is currently a 12th grader at the Livingston High School. He is a dedicated singer-student-athlete with a passion for Math and Physics who is fascinated with data analysis and calculations related to aerospace. He founded his high school’s Rocketry Club, competing in the American Rocketry Challenge and also holding educational community launches to spark interest in rocketry and aerospace. Alex has been a part of his school’s Math Team for all four years of high school, and rising to the Math Honor Society’s Vice President in his Junior year. He was also a camp counselor at the Delaware Aerospace Academy, teaching young students about aviation, space, and rockets. He taught the students to construct and launch model rockets, maglev trains, and solar robots.
In addition to these activities, Alex also plays varsity baseball for his school, being the starting second baseman and starting shortstop in his sophomore and junior years respectively. He has also been an active singer, singing in his school chorus, select chorus, and an outside volunteer chorus. He has auditioned into the NJ All-State Chorus both of the last two years, and he is currently ranked 6th in the state in the Tenor 1 voice part. He is deeply interested in math, data science, physics, and computer science and would like to apply his math and physics knowledge to improve technology. Alex looks to further his knowledge and interest in STEM by studying data science related topics in higher education.
